Why Sir took minimum of that one? In 2 cases

#1

Why Sir took minimum of that one? In 2 cases

#2

Hello @cbcao263

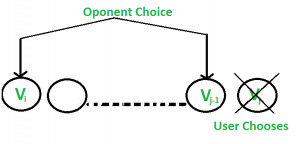
There are two choices:

  1. The user chooses the ith coin with value Vi: The opponent either chooses (i+1)th coin or jth coin. The opponent intends to choose the coin which leaves the user with minimum value.
    i.e. The user can collect the value Vi + min(F(i+2, j), F(i+1, j-1) )

image
image721×315 4.4 KB

  1. The user chooses the jth coin with value Vj: The opponent either chooses ith coin or (j-1)th coin. The opponent intends to choose the coin which leaves the user with minimum value.
    i.e. The user can collect the value Vj + min(F(i+1, j-1), F(i, j-2) )
    image

Following is recursive solution that is based on above two choices. We take the maximum of two choices.

F(i, j) represents the maximum value the user can collect from
i’th coin to j’th coin.

F(i, j) = Max(Vi + min(F(i+2, j), F(i+1, j-1) ),
Vj + min(F(i+1, j-1), F(i, j-2) ))

Base Cases

F(i, j) = Vi If j == i
F(i, j) = max(Vi, Vj) If j == i+1

explanation:
Let’s understand this:
let the index at which the leftmost coin is available be l (initially 0)
and the index at which the rightmost coin is available be r (initially n-1)

  1. if piyush chooses l
    then in the next pick he will have two possible choices:
    (l-1,r-1): the opponent has selected the rightmost coin
    (l-2,r): the opponent has selected the leftmost coin.
    sum= arr[l]+min(fun(l-1,r-1),fun(l-2,r))
    opponent will choose something that will cause piyush to have minimum sum.
  2. if piyush chooses r
    then in the next pick he will have two possible choices:
    (l-1,r-1): the opponent has selected the leftmost coin
    (l,r-2): the opponent has selected the rightmost coin.
    sum= arr[r]+min(fun(l-1,r-1),fun(l,r-2))
    opponent will choose something that will cause piyush to have minimum sum.

Hope, this would help.

#3

I hope I’ve cleared your doubt. I ask you to please rate your experience here
Your feedback is very important. It helps us improve our platform and hence provide you
the learning experience you deserve.

On the off chance, you still have some questions or not find the answers satisfactory, you may reopen
the doubt.