Please solve these doubts related to Quiz on graphs

#1
  1. If we use trees with the union-by-rank algorithm, what is the worst case running time for checking if two elements are in same set or not?

O(1)

O(n)

O(logN)

O(N^2)
Here because we have not applied path-compression, shouldn’t it be O(n)

  1. What is the maximum number of edges in the maximum matching of a bipartite graph with n vertices?

n

n^2

n/2

  1. Time Complexity Of Kruskals Algorithm(Here E is the number of edges and V are the number of vertices)
    a) O(ElogV)
    b) O(Elog√E)
    c) O((V^2)log(E^2) + Elog(V^2)) d)
    d) O(ElogE + Elog(V^2))

A, B are correct

Only A is correct

B, C, D are correct

A, B, D are correct
Only A should be correct.

  1. Q4. Topological Sort
    What will be topological sort order of the following graph

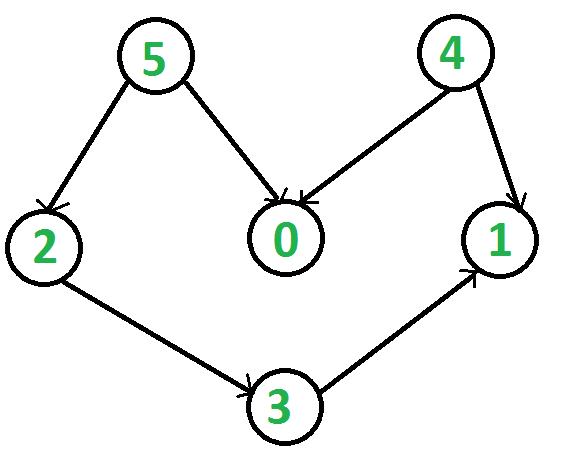
    5 4 2 3 0 1

5 4 2 3 1 0

5 4 2 0 1 3

5 2 3 1 4 0

Should’nt it be 5 4 2 0 1 3?

  1. How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?

(n(n-1))/2

n!

2^((n*(n-1))/2)

2^n

  1. What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?

1

2

n

n-1

3

  1. How many simple undirected non-isomorphic graphs are there with 4 vertices?

8

32

4

64

#2

hello @sahilkhan2312000131
…

no , it will be log(n), in union by rank tree height will not exceed log(n).

#3

it will be n/2 * n/2 = n*n/4

i.e put n/2 vertex in one set and rest n/2 in other set

and then from each other from one set create an edge to n/2 vertices of other set.

#4

…

hint -> use log property and E = V^2 in worst case

2^(n*(n-1)/2)

total n*(n-1)/2 edges will be there in complete graph.
now we have option on each edges , wheter to include it or discard it.
hence 2^(n*(n-1)/2)

#5

Please answer these also:
6. What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?

1

2

n

n-1

3

  1. How many simple undirected non-isomorphic graphs are there with 4 vertices?

8

32

4

64

#6

…

A graph is connected and has ‘nn’ vertices and edges means, exactly one cycle is there.

Now we can make a different spanning tree by removing one edge from the cycle, one at a time.

Minimum cycle length can be 3, So, there must be at least 3 spanning trees in any such graph.

pls read about non isomorphic graphs and then attempt this question

#7

I hope I’ve cleared your doubt. I ask you to please rate your experience here
Your feedback is very important. It helps us improve our platform and hence provide you
the learning experience you deserve.

On the off chance, you still have some questions or not find the answers satisfactory, you may reopen
the doubt.

#8
  1. What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?

1

2

n

n-1

3
shouldn’t it be n-1

#9

minumum cycle possible is of length 3.
so least m will be 3.

maximum it will be n-1

#10

I hope I’ve cleared your doubt. I ask you to please rate your experience here
Your feedback is very important. It helps us improve our platform and hence provide you
the learning experience you deserve.

On the off chance, you still have some questions or not find the answers satisfactory, you may reopen
the doubt.