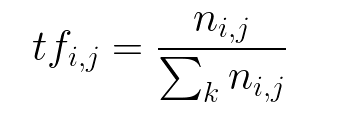Multinomial Naive Bayes

#1

Sir used in the formula in the denominator : Summation of " d belonging to c "

as the total number of docs belonging to class C.

Shouldn’t be it the total number of words in each document belonging to class C because it feels like a specific term in a document can outnumber the total number of documents which will make Num > Den

If " tf( t, d) " represents NORMALIZED TERM FREQ. then only this is formula seems correct.

#2

Hey @mananaroramail, actually normalized term frequency, is equal to the number of times a word appears in a document divded by the total number of words in the document. Every document has its own term frequency.

This is the formula for normalized term frequency.

Hope this resolved your doubt.
Plz mark the doubt as resolved in my doubts section. :blush:

#3

So, the final formula is :
Here S = Sigma

[S tf( xi | y=c ) + alpha] / [S ( d belongs to c ) + alpha*|Vocab| ]

This formula was used in Multinomial Naive Bayes

So, what is " tf( xi | y=c ) ".
According to what I understood : It is the sum of term frequency ( AND NOT NORMALIZED TERM FREQ. ) of the term " xi " where the document class == c

Then what is " S ( d belongs to c ) " ??
Is it the total words in the document where the document belongs to class c or it is the total number of documents where documents class == c.

In the video, it was " it is the total number of documents where documents class == c " but what it actually meant was unclear as it feels like Num may become larger than the Den.

Can you please define these terms of the formula

#4

Hey @mananaroramail, your denominator term is equal to ‘count of all words belonging to documents belonging to class ==c’.

Hope now you get it.

#5

Ok, I get it. One thing more :

And this is just the frequency of the feature " xi " while traversing over all the documents where the class of the document is c ??

#6

Hey @mananaroramail, yes you are right.

#7

I hope I’ve cleared your doubt. I ask you to please rate your experience here
Your feedback is very important. It helps us improve our platform and hence provide you
the learning experience you deserve.

On the off chance, you still have some questions or not find the answers satisfactory, you may reopen
the doubt.