why large values of log likelihood means that model is a poor fit to data?
Logistic regression log likelihood
Lets first understand what a good fitting model of your data means. A good fitting model is the one that when used for testing or validating has a good accuracy of prediction, i.e, most of the time, it predicts the correct label of an instance under supervised learning criterion. So, if we need a model that is a good fit of our data, we need to tell the model (while training) that, its making a mistake in predicting a label or not. If it does make a mistake, we need to make it correct by some means.
Now, technically, the way we say that a model is making mistake in predicting is through “log loss or log likelihood” and the means by which we tell the model to correct its mistake is “gradient descent”.
Now coming to your question, why large values of log likelihood means that model is a poor fit to data, rephrasing, why large values of log likelihood means that our model is not predicting correct labels to our data.
To understand this, lets look at the graph of log(x) :
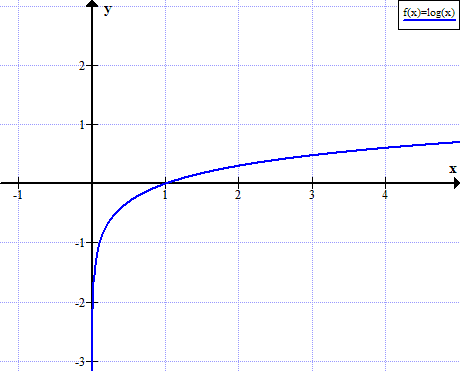
if you carefully look at this graph, you can infer for a fact that when the value of x is near 0, the value of log(x) is very negative while when x is near 1, log(x) is near 0. Similarly, if we take the graph of -log(x), when x is near 0, the value of log(x) becomes very high(positive) while when x is near 1, log(x) is near 0.
Exploiting this fact, we came up with log likelihood(for binary classification), which is:
J = y * -log(p(x)) + (1 - y) * -log(1 - p(x)), where J is the loss of our model and p is the probability of y being 1.
Lets now see what will be the value of J when y = 1 and our model predicted 1 (correct prediction),
J = 1 * -log(1) + (1 - 1) * -log(1 - 1) = 0
Also, when y = 1 and our model predicted 0 ( wrong predicition),
J = 1 * -log(0) + (1 - 1) * -log(1 - 0) = -log(0) = -(-inf) = inf or very high value.
Similarly, J can be calculated when y = 0 and p(x) = 1 and y = 0 and p(x) = 0.
In all these cases, you will see that when the model makes a wrong prediction, the value of log likelihood is very high inferring that our model is a poor fit to our data.
I hope you got the intuition behind why log likelihood is used as a loss for learning and why high values of it infers poor fitting of data.
If the answer resolved your query, be sure to mark it resolved. 
Happy Learning,

